4.1 Modelo conceitual
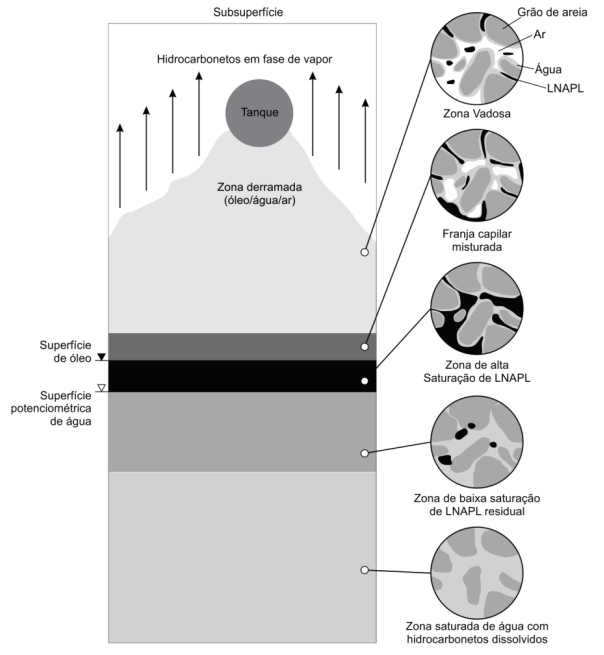
A figura abaixo mostra um vazamento de hidrocarbonetos de petróleo de um tanque subterrâneo. Esses hidrocarbonetos, que são mais leves que a água e não se misturam com ela, descem pelo solo devido à gravidade e se espalham lateralmente. Parte do líquido fica presa no solo como resíduo, enquanto outra parte evapora.
Quando o nível da água subterrânea sobe e desce, o hidrocarboneto residual se mistura mais com a água, aumentando a contaminação. Essa contaminação se move pelo aquífero devido ao fluxo da água e à dispersão.
Entender o movimento e a persistência do LNAPL (líquido leve de fase não aquosa) é essencial para avaliar áreas contaminadas. Vários fatores influenciam esse processo, como o tipo de solo, a quantidade de líquido derramado e as características do hidrocarboneto. O LNAPL pode se mover se houver uma fase contínua do líquido no solo e sua saturação for alta, enquanto o LNAPL residual pode continuar a contaminar a água por muito tempo.
A modelagem matemática e a simulação computacional do comportamento do LNAPL após um derramamento no solo são complexas e têm sido estudadas extensivamente. Pesquisadores utilizam equações matemáticas para descrever o fluxo multifásico e o transporte de compostos orgânicos em solos. Estas equações são resolvidas usando técnicas de diferenças finitas e elementos finitos, além de modelos específicos para a interação entre o ar, LNAPL e água na zona não saturada do solo.
A proposta da USEPA (1997) inclui a descrição do fluxo do LNAPL nas zonas vadosa (não saturada), úmida (franja capilar) e saturada (aquífero). Modelos numéricos simulam as fases móveis (água, LNAPL e gás) assumindo que o solo é rígido e estático. O LNAPL pode existir como líquido puro, dissolvido ou vapor, e pode ficar imobilizado nos poros do solo ou adsorvido na matéria orgânica.
Para modelar matematicamente o fenômeno, utiliza-se um volume representativo do solo e desenvolvem-se equações de balanço de massa para as fases líquidas e gasosas. Essas equações consideram as propriedades dos fluidos, advecção, dispersão, difusão e trocas de massa entre as fases. A solução dessas equações, dadas as condições iniciais e de contorno, fornece a distribuição do volume, pressão e concentração dos constituintes no tempo e espaço.
A complexidade do modelo pode ser simplificada dependendo das características do solo e do derramamento. Por exemplo, em solos arenosos com pouca matéria orgânica, a ação capilar é menor e o LNAPL residual é reduzido, permitindo simplificações no modelo. As propriedades do solo, como porosidade e permeabilidade, e as constantes físicas dos fluidos são fundamentais para resolver as equações.
O modelo da USEPA (1997), denominado de NAPL Simulator, e outros similares fornecem uma base para entender e prever o comportamento do LNAPL em diferentes condições de campo, auxiliando na análise e mitigação de contaminações.
4.2 Propriedades do Fluido
Densidade, Viscosidade Dinâmica, Viscosidade Cinemática e Mobilidade
A densidade dos fluidos (ρ) reflete a ação da aceleração da gravidade (g), e a viscosidade dinâmica (μ) indica a resistência ao esforço de cisalhamento. A razão μ/ρ é chamada de viscosidade cinemática (ν) e influencia diretamente o fluxo dos fluidos. A mobilidade de um fluido é indicada pela relação ρg/μ, chamada de coeficiente de mobilidade, e é usada para classificar a mobilidade dos líquidos em meios porosos ou tubulares.
Componentes da gasolina (BTEX: benzeno, tolueno, etilbenzeno e xileno) possuem maior mobilidade que a água, chegando mais rápido ao lençol freático devido a essa característica. Por serem menos densos e pouco solúveis, flutuam sobre o lençol freático. Já os hidrocarbonetos halogenados, mais densos que a água, continuam a descer até encontrarem uma barreira impermeável.
Tensão Superficial e Interfacial
A tensão na interface de um fluido com seu vapor é chamada de tensão superficial (σ). Fluidos com maior tensão superficial espalham-se mais no solo, resultando em maior saturação residual. Por exemplo, a água (σ = 72,8 dina/cm) espalha-se mais facilmente no solo do que o benzeno (σ = 22,9 dina/cm).
A tensão interfacial (σ) ocorre na interface entre fluidos não miscíveis, sendo menor do que a maior tensão superficial dos líquidos envolvidos. É crucial para entender sistemas multifásicos, como as interfaces líquido-líquido ou líquido-sólido.
Adsorção, Espalhamento do Líquido sobre o Solo, Molhabilidade e Ângulo de Contato
A molhabilidade descreve como um líquido se espalha no meio poroso, influenciada pelas tensões superficiais e interfaciais. O ângulo de contato, descrito por Hillel (1980), forma-se entre a gota do líquido e a superfície sólida. Se as forças de adesão entre o sólido e o líquido são maiores que as de coesão do líquido, o ângulo é agudo, e o líquido molha o sólido.
A tensão de adesão (σ) determina qual fluido molhará preferencialmente a superfície sólida. Um ângulo de contato pequeno indica que a fase aquosa irá se espalhar sobre a superfície. Se o ângulo for grande, será necessária uma fonte de energia externa para espalhar a fase aquosa.
Ao colocar uma gota de água sobre vidro limpo, a água se espalha devido à alta afinidade. Em contraste, sobre teflon, a água forma uma bolha devido à baixa afinidade superficial, não molhando preferencialmente o teflon. Assim, a molhabilidade relativa dos fluidos determina a tendência de um fluido deslocar outro numa superfície sólida.
4.3 Relações permeabilidade, saturação e sucção matricial k-S-P
Na zona não saturada, onde coexistem solo, ar e líquidos, os mecanismos de fluxo e transporte envolvem pressões capilares e adsorção, responsáveis pela retenção de líquidos pelo solo. Tanto a capilaridade quanto a adsorção reduzem a energia livre do líquido, resultando em menor potencial energético do líquido em solos mais secos. Isso explica a movimentação da água de uma área úmida para uma seca no solo, contra o potencial gravitacional. Essa diferença de energia gerada pelos fenômenos de capilaridade e adsorção cria gradientes hidráulicos que succionam a água para o solo, representada pela sucção matricial (Y), definida como a diferença de pressão entre a fase não molhante e a fase molhante, sempre com valores positivos.
A energia do líquido no solo não saturado é função de seu conteúdo no solo, tornando necessário determinar as relações funcionais da sucção matricial (Y) com a permeabilidade (k) e a saturação (S), conhecidas como relações k-S-P. Devido à não linearidade dessas relações, o fluxo no meio poroso não saturado possui um comportamento altamente não linear. Embora essas relações sejam cruciais na migração de LNAPL (Líquidos Não Aquosos de Petróleo) em solo não saturado, há uma escassez de dados experimentais devido à dificuldade experimental para medi-los em um sistema trifásico. Assim, a modelagem do fluxo trifásico tem recorrido a métodos que adaptam as relações k-S-P estabelecidas para sistemas bifásicos para representar um sistema trifásico, conforme metodologias sugeridas por Leverett (1941) e Parker et al. (1987).
- Saturação (S)
Em condições de não saturação, como em um sistema bifásico de água e ar, a porosidade total é definida como a soma dos conteúdos volumétricos da água e do ar. A saturação (S) expressa a relação entre o conteúdo volumétrico de uma espécie nos poros de um solo e a porosidade do meio. É a fração ocupada por essa fase. Para um sistema trifásico de LNAPL-gás-água no solo, a soma das saturações de todas as fases deve ser igual a 1 (100%).
- Curva característica do solo (S-P)
A curva característica do solo (S-P) varia conforme o tipo de solo, desde areia até argila, cada um apresentando uma curva de retenção distinta. Solos com maior predominância de macroporos, como as areias, removem quase todo o líquido intersticial mesmo em baixas sucções, enquanto solos argilosos requerem sucções elevadas para remover o líquido de seus poros. Diversas técnicas experimentais, como placas de pressão e ensaios de papel-filtro, são utilizadas para medir a relação P-S em amostras de solo. A dependência da sucção com a saturação do solo resulta na histerese da curva característica, onde diferentes trajetórias de drenagem e umedecimento levam a valores diferentes de saturação para uma mesma sucção.
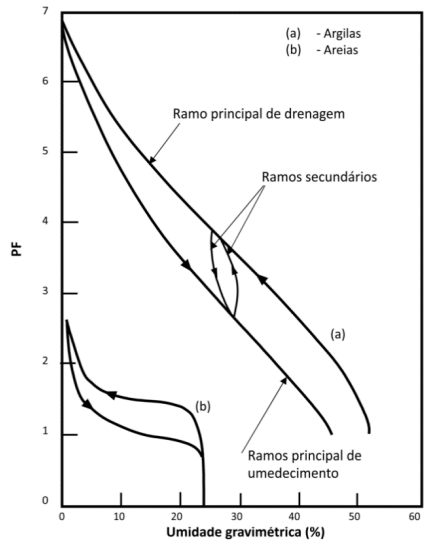
Na modelagem matemática de processos de fluxo multifásico, como o derramamento de LNAPL, são utilizados modelos como os de Brooks e Corey (1964) e de van Genuchten (1980) para representar a relação entre sucção e saturação. O modelo de Brooks e Corey normaliza os conteúdos volumétricos do líquido molhante em termos da saturação efetiva e os relaciona com a sucção matricial, considerando parâmetros como umidade residual e pressão de entrada de ar. O modelo de van Genuchten descreve a saturação efetiva como função da sucção e foi adaptado por Leverett (1941) e Schiegg (1984) para estimar sucções em sistemas bifásicos como LNAPL-gás e LNAPL-água em solos arenosos. Parker et al. (1987) também propuseram uma forma generalizada da equação de van Genuchten para sistemas bifásicos. Esses modelos não consideram as diferentes interações solo/fluido, como a adsorção diferencial de fluidos com diferentes polaridades pela fração argilosa do solo.
- Coeficiente de permeabilidade relativa (k-S)
Em sistemas multifásicos, a permeabilidade relativa é crucial para descrever o fluxo simultâneo dos fluidos no meio poroso. Ela incorpora diversos efeitos, como a geometria dos poros, características de molhabilidade, distribuição do fluido, saturação e velocidade de fluxo das fases, que por sua vez dependem da viscosidade, massa específica, tensão interfacial e constante dielétrica dos fluidos. As curvas típicas de permeabilidade relativa em função da saturação mostram a dependência dessa permeabilidade com o grau de saturação de cada fluido. Por exemplo, a permeabilidade relativa do fluido molhante se torna zero em uma determinada saturação, chamada de saturação residual, e a do fluido não molhante se torna zero em outra saturação, chamada de saturação irredutível.
Devido às dificuldades experimentais, há poucos dados para permeabilidade relativa trifásica, sendo comum usar métodos de estimativa com base em dados experimentais da relação S-P. Modelos como os de Burdine e Brooks e Corey fornecem equações para permeabilidade relativa de água (Krw) e LNAPL (Krn). A partir dessas equações, é possível estimar a saturação mínima ou residual de ar (Sar) na zona não saturada, um parâmetro importante na modelagem, pois limita a permeabilidade máxima efetiva da fase LNAPL.
4.4 Modelo simplificado para o fluxo do LNAPL na zona não saturada
Modelos matemáticos são ferramentas cruciais para prever o transporte de contaminantes na zona não saturada do solo, ajudando na tomada de decisões sobre controle e remediação. Em condições simplificadas de fluxo multifásico, esses modelos podem ser substituídos por equações analíticas ou semianalíticas.
Estudos como o de Oliveira (1995) testaram vários modelos analíticos em laboratório para simular o fluxo de líquidos orgânicos em colunas de areia. Modelos como os de Green e Ampt (1911) e Philip (1969) mostraram-se adequados para modelar o fluxo unifásico e unidimensional desses líquidos. Recentemente, Sousa (2012) demonstrou que o modelo de Philip (1969) pode prever a componente vertical do fluxo bidimensional de um LNAPL, desde que a condutividade hidráulica utilizada seja a do solo insaturado.
Essas equações, originalmente desenvolvidas para fluxo unifásico, podem ser adaptadas para fluxo bifásico com modificações nas propriedades de transporte, como a dependência da capilaridade da tensão interfacial líquido-líquido e da condutividade hidráulica da permeabilidade relativa. Além disso, podem ser facilmente adaptadas para cálculos semianalíticos em situações como variação da condutividade hidráulica do solo ou da pressão hidrostática na superfície ao longo do tempo, como em casos de vazamentos.
